This will be the first in a series of tutorials covering a few of the fundamental topics in statistical analysis and machine learning.

K-Means and Clustering

Basic Problem and Clustering

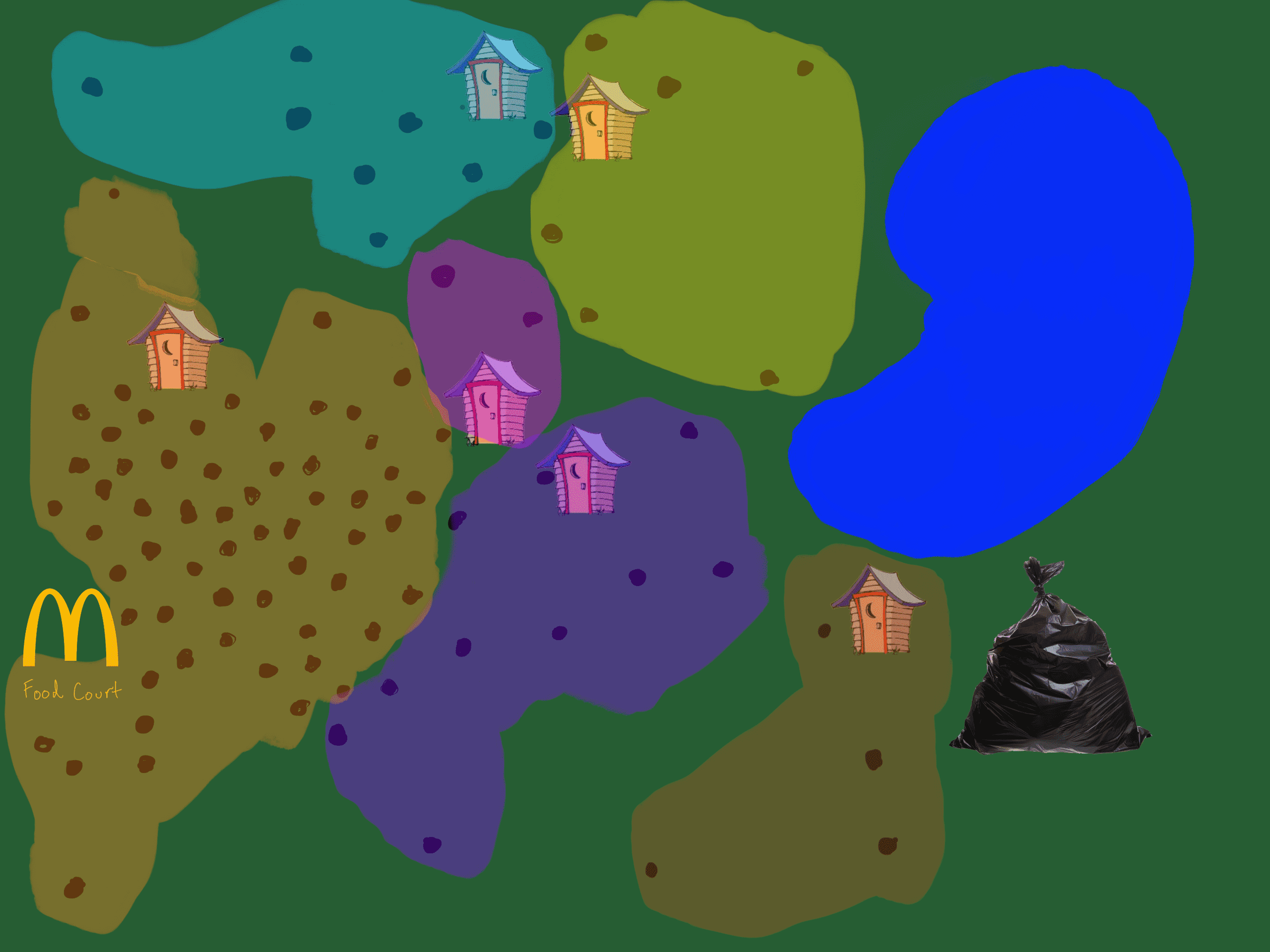
You've built a theme park (congrats btw). The park is already open, but you somehow omitted restrooms in the design of the park (why'd you do that). Things are getting... messy.

You know you need to build a ton of bathrooms as fast as possible. Here's the problem, you can only afford 6 bathrooms. Your advisors are telling you to place the bathrooms equidistantly, so the distribution is uniform across the park. At first, this seems like the best solution, but then you notice a fatal flaw in the plan (makes up for the restroom debacle). Although the bathrooms are equidistant, this is not a meaningful distribution. The bathrooms should be placed in a way, that reflects the common distribution of people in the park. The advisors suggested method places only 1 bathroom at the food court (you've already been reported to health department, you can't afford another incident).

The black dots are people, you're abstract.

You realize there is a much better method for placing the bathrooms. The primary investor in your theme park was Facebook. One of the requirements of taking their money, was that your park be equipped with the highly advanced "Facebook happiness monitoring system". The system allows you (and Facebook) to monitor the location of every attendee in the park, at all times. There's even an app that lets you view everyone on a map. Technology is neat!

You place the bathrooms on the map. Your goal is to place them in a way, that minimizes the average distance that any random attendee is from a bathroom.

Example, if half of the park (in terms of sq ft) is constantly vacant, the new method would place 0 bathrooms in the vacant area.

Now, bathrooms are placed uniformly across the areas of the park that are most populated. Things are less messy! K-means, essentially boils down to the process you used to place the bathrooms in the park (see, you knew it all along)

Aside: In this case, simple k-means would not be enough. Although the placement is a huge improvement over the advisors suggestion, the food court still only has 1 bathroom. To solve that problem, we would need to add a constraint to the k-means algorithm that limits the max attendees that can be associated with a single bathroom. This way, areas that are incredibly dense, will receive bathrooms proportionate to their density.

K-Means Phases

Now that you understand the problem that k-means is trying to solve. Let's go over how the algorithm is implemented at a high level. There are really two distinct phases of k-means.

• Centroid Initialization Phase
• Iterative Phase

Centroid Initialization

When the k-means algorithm begins, no centroids (bathrooms) have been placed in the data space (theme park). In the case of the theme park, the amount of people was few enough, that it was practical to "eyeball it". But this does not scale, eventually, when your data set is large enough or in higher dimensions, it becomes impossible to "eyeball" it.

K-Means centroid initialization is a field of research itself. There's a lot of ways to handle it, but for now, you keep it simple. You initially place each of the bathrooms at a random attendees position (this isn't a wicked witch situation, you moved the attendee).

Randomly placed

Iterations

You've done the initial bathroom placement with the random positions, and it turned out better than you thought. Although, you had never considered having a bathroom so close to the dumpsters before.

You still think you can do better. Instead of just throwing darts at a dartboard again (like you did with the initialization you psycho), you want to tackle it more thoughtfully. You decide that attendees will be divided into groups, each group representing a bathroom that the attendee is closest to.

Closest bathroom zones, It's rough.

Once you have the groups figured out, you compute per-group attendee averages. This gives you the average position of an attendee in each resulting bathroom group. Next, you pay a construction crew to move each of the bathrooms, to the average group locations you just calculated. This improves your bathroom placement, but doesn't fix it entirely.

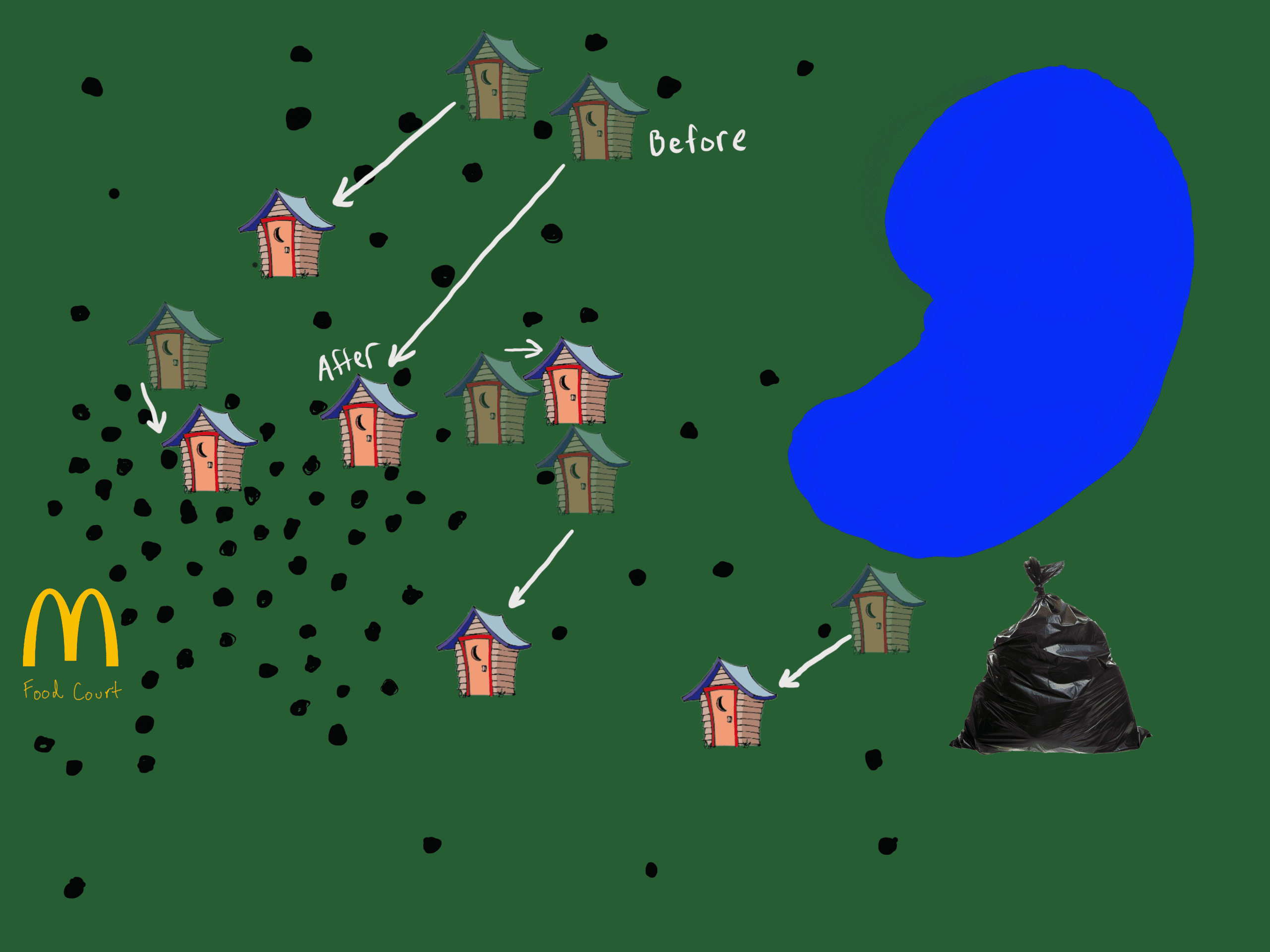
The first move

You tell your investors, if you can move the bathrooms just one more time, it will fix the problem. ~50 costly bathroom reconstructions later, you think you've found the "best" location for each bathroom. Allegedly, a person on average will always be as close to the bathroom as they can!

The 50th move

In your infinite wisdom you also make another observation. You're currently dividing the attendees into k (# of bathrooms) groups and averaging them. You realize the algorithm is named "k-means" because you are taking the means (averages) of k groups. How smart!

Convergence

You really believe the bathrooms are placed correctly now (only took 50 tries), but to guarantee the cleanliness of the park, your investors are requiring you to prove it.

You start thinking (never a good sign), how can you be sure the bathroom placement is really "optimal"? You decide to repeat the process you employed in the Iterations section, and once again measure the distances and move the bathrooms. You make an observation: for each adjustment made to the bathrooms locations, the amount the locations adjust decreases. In fact, by move #55, the bathrooms only shift a couple inches after being adjusted based on the grouped attendee averages.

You've already dumped half your runway money into this bathroom venture, will anyone ever take you seriously if you don't follow through to the end? You decide to do a few more measurements and reconstructions, but something very strange happens (X-files music), the bathrooms seem to not be moving anymore. In fact, no matter how many times you redo the calculations, the bathroom locations stay identical to the corresponding group averages.

Convergence

When this happens during the k-means algorithm, it is referred to as "convergence". Convergence signifies that further iterations to the k-means algorithm will never again lead to a change, you're done.

Well not quite done, unfortunately, convergence does still not guarantee you've "optimally" placed the bathrooms. For example, if you were to have started with the bathrooms in a different configuration, it may have resulted in a better convergence. The placement will have to be good enough for now, you're broke (what a business mastermind)!

Conclusion

This was a very high level overview of a simple k-means algorithm. There's traditionally a lot of work that goes into initial placement of centroids (bathrooms), and this can have a huge impact on the outcome.

The next article will cover k-means from a programming perspective, through implementing a simple version of the algorithm in Python or JavaScript. Future articles will cover centroid initialization approaches, k-means parallelization and optimization, and other progressively advanced k-means topics.